Menguasai Matematika Kelas 7 Semester 2: Panduan Lengkap dengan Contoh Soal dan Pembahasan Mendalam

Semester 2 di kelas 7 SMP merupakan periode penting dalam perjalanan belajar matematika. Materi yang diajarkan semakin mendalam dan aplikatif, menuntut pemahaman konsep yang kuat serta kemampuan memecahkan masalah yang lebih kompleks. Artikel ini hadir untuk membantu Anda menguasai materi matematika kelas 7 semester 2 melalui contoh soal yang relevan dan pembahasan yang terperinci. Dengan pemahaman yang baik, Anda akan lebih percaya diri dalam menghadapi berbagai tantangan matematika.

Pentingnya Memahami Materi Semester 2 Kelas 7

Materi matematika kelas 7 semester 2 menjadi fondasi penting untuk materi-materi di jenjang selanjutnya. Konsep-konsep yang dipelajari akan terus berkembang dan menjadi prasyarat untuk pemahaman yang lebih lanjut. Oleh karena itu, menguasai materi ini secara tuntas akan memberikan keuntungan besar dalam perjalanan akademis Anda.

Topik Utama Matematika Kelas 7 Semester 2

Semester 2 kelas 7 umumnya mencakup beberapa topik utama yang saling berkaitan. Berikut adalah beberapa di antaranya, beserta contoh soal dan pembahasannya:

1. Bentuk Aljabar

Bentuk aljabar adalah salah satu konsep fundamental dalam matematika. Memahami notasi, variabel, koefisien, dan konstanta akan membuka pintu ke berbagai aplikasi matematika.

• Konsep Kunci:

  • Variabel: Simbol yang mewakili nilai yang tidak diketahui (misalnya, $x$, $y$, $a$).
  • Koefisien: Angka yang mengalikan variabel (misalnya, pada $3x$, koefisiennya adalah $3$).
  • Konstanta: Bilangan yang berdiri sendiri, tidak memiliki variabel (misalnya, pada $2y + 5$, konstannya adalah $5$).
  • Suku Sejenis: Suku-suku yang memiliki variabel dan pangkat variabel yang sama.
  • Menyederhanakan Bentuk Aljabar: Menggabungkan suku-suku sejenis.
  • Menjumlahkan dan Mengurangkan Bentuk Aljabar: Menjumlahkan atau mengurangkan koefisien dari suku-suku sejenis.
  • Perkalian Bentuk Aljabar: Mengalikan koefisien dan menjumlahkan pangkat variabel.

• Contoh Soal 1:
  Sederhanakan bentuk aljabar berikut: $5a + 3b – 2a + 7b$

  Pembahasan:
  Langkah pertama adalah mengidentifikasi suku-suku sejenis. Suku-suku yang memiliki variabel $a$ adalah $5a$ dan $-2a$. Suku-suku yang memiliki variabel $b$ adalah $3b$ dan $7b$.
  Kemudian, kita gabungkan suku-suku sejenis tersebut:
  $(5a – 2a) + (3b + 7b)$
  $3a + 10b$

  Jadi, bentuk aljabar yang disederhanakan adalah $3a + 10b$.

• Contoh Soal 2:
  Tentukan hasil perkalian dari $(2x + 3)(x – 4)$.

  Pembahasan:
  Untuk mengalikan dua bentuk aljabar, kita bisa menggunakan metode distributif (atau sering disebut metode FOIL: First, Outer, Inner, Last).

  • First (Pertama): $2x times x = 2x^2$
  • Outer (Luar): $2x times (-4) = -8x$
  • Inner (Dalam): $3 times x = 3x$
  • Last (Terakhir): $3 times (-4) = -12$

  Sekarang, kita jumlahkan hasil perkalian tersebut:
  $2x^2 – 8x + 3x – 12$
  Kemudian, sederhanakan dengan menggabungkan suku-suku sejenis (yaitu, suku-suku yang memiliki variabel $x$):
  $2x^2 + (-8x + 3x) – 12$
  $2x^2 – 5x – 12$

  Jadi, hasil perkalian dari $(2x + 3)(x – 4)$ adalah $2x^2 – 5x – 12$.

2. Persamaan Linear Satu Variabel

Persamaan linear satu variabel adalah persamaan di mana hanya ada satu variabel dan pangkat tertingginya adalah satu. Menyelesaikan persamaan ini berarti mencari nilai variabel yang membuat persamaan tersebut benar.

• Konsep Kunci:

  • Persamaan: Pernyataan matematika yang menyatakan bahwa dua ekspresi memiliki nilai yang sama, ditandai dengan simbol sama dengan ($=$).
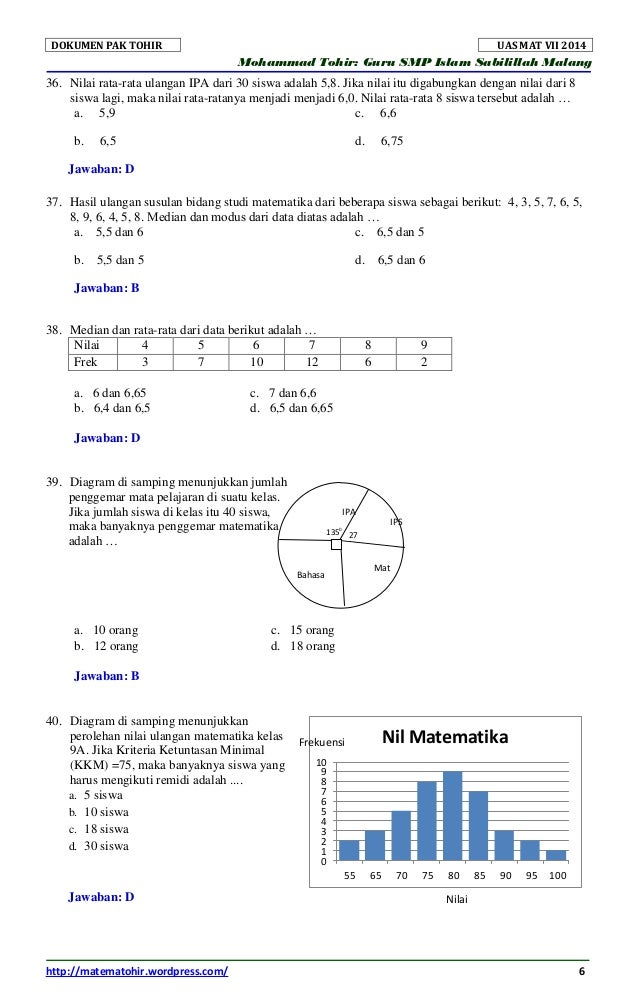
  • Variabel: Simbol yang mewakili nilai yang tidak diketahui.
  • Menyelesaikan Persamaan: Mencari nilai variabel yang memenuhi persamaan.
  • Prinsip Kesetaraan: Apapun operasi yang dilakukan pada satu sisi persamaan, harus dilakukan juga pada sisi lainnya agar kesetaraan tetap terjaga. Ini meliputi penambahan, pengurangan, perkalian, dan pembagian dengan bilangan yang sama (selain nol).

• Contoh Soal 3:
  Tentukan nilai $x$ dari persamaan: $3x + 5 = 14$

  Pembahasan:
  Tujuan kita adalah mengisolasi variabel $x$ di salah satu sisi persamaan.

  1. Kurangi kedua sisi persamaan dengan $5$:
     $3x + 5 – 5 = 14 – 5$
     $3x = 9$
  2. Bagi kedua sisi persamaan dengan $3$:
     $frac3x3 = frac93$
     $x = 3$

  Jadi, nilai $x$ yang memenuhi persamaan $3x + 5 = 14$ adalah $3$.

• Contoh Soal 4:
  Selesaikan persamaan berikut untuk nilai $y$: $frac12y – 3 = 7$

  Pembahasan:

  1. Tambahkan $3$ ke kedua sisi persamaan:
     $frac12y – 3 + 3 = 7 + 3$
     $frac12y = 10$
  2. Kalikan kedua sisi persamaan dengan $2$ untuk menghilangkan pecahan:
     $2 times frac12y = 2 times 10$
     $y = 20$

  Jadi, nilai $y$ yang memenuhi persamaan $frac12y – 3 = 7$ adalah $20$.

3. Pertidaksamaan Linear Satu Variabel

Pertidaksamaan linear satu variabel mirip dengan persamaan linear, namun menggunakan simbol ketidaksamaan seperti $<$, $>$, $le$, atau $ge$. Solusinya biasanya berupa rentang nilai.

• Konsep Kunci:

  • Pertidaksamaan: Pernyataan matematika yang membandingkan dua ekspresi menggunakan simbol ketidaksamaan.
  • Menyelesaikan Pertidaksamaan: Mencari rentang nilai variabel yang memenuhi pertidaksamaan.
  • Perhatian pada Perkalian/Pembagian dengan Bilangan Negatif: Jika kedua sisi pertidaksamaan dikalikan atau dibagi dengan bilangan negatif, arah simbol ketidaksamaan harus dibalik.

• Contoh Soal 5:
  Tentukan himpunan penyelesaian dari pertidaksamaan: $2x – 4 < 6$

  Pembahasan:

  1. Tambahkan $4$ ke kedua sisi pertidaksamaan:
     $2x – 4 + 4 < 6 + 4$
     $2x < 10$
  2. Bagi kedua sisi pertidaksamaan dengan $2$:
     $frac2x2 < frac102$
     $x < 5$

  Jadi, himpunan penyelesaiannya adalah semua bilangan real $x$ yang kurang dari $5$. Dalam notasi himpunan, bisa ditulis $x mid x < 5$.

• Contoh Soal 6:
  Selesaikan pertidaksamaan berikut: $-3x + 1 ge 7$

  Pembahasan:

  1. Kurangi $1$ dari kedua sisi pertidaksamaan:
     $-3x + 1 – 1 ge 7 – 1$
     $-3x ge 6$
  2. Bagi kedua sisi pertidaksamaan dengan $-3$. Penting: Karena kita membagi dengan bilangan negatif, kita harus membalik arah simbol ketidaksamaan.
     $frac-3x-3 le frac6-3$
     $x le -2$

  Jadi, himpunan penyelesaiannya adalah semua bilangan real $x$ yang kurang dari atau sama dengan $-2$. Dalam notasi himpunan, bisa ditulis $x mid x le -2$.

4. Perbandingan dan Skala

Perbandingan digunakan untuk membandingkan dua kuantitas, sedangkan skala digunakan dalam peta, denah, atau model untuk merepresentasikan ukuran sebenarnya.

• Konsep Kunci:

  • Perbandingan: Bentuk sederhana dari dua atau lebih kuantitas. Dapat ditulis dalam bentuk $a:b$ atau $fracab$.
  • Skala: Perbandingan antara ukuran pada model/peta dengan ukuran sebenarnya. Biasanya ditulis dalam bentuk $1 : n$, yang berarti $1$ unit pada model mewakili $n$ unit pada kenyataan.
  • Menghitung Ukuran Sebenarnya atau Ukuran Model: Menggunakan perbandingan skala.

• Contoh Soal 7:
  Perbandingan panjang dan lebar sebuah lapangan futsal adalah $5:3$. Jika panjang lapangan tersebut adalah $40$ meter, berapakah lebarnya?

  Pembahasan:
  Misalkan panjang lapangan adalah $P$ dan lebar lapangan adalah $L$. Diketahui $P:L = 5:3$, atau $fracPL = frac53$.
  Kita juga tahu $P = 40$ meter. Substitusikan nilai $P$ ke dalam persamaan:
  $frac40L = frac53$
  Untuk mencari $L$, kita bisa melakukan perkalian silang:
  $40 times 3 = 5 times L$
  $120 = 5L$
  Bagi kedua sisi dengan $5$:
  $L = frac1205$
  $L = 24$ meter.

  Jadi, lebar lapangan futsal tersebut adalah $24$ meter.

• Contoh Soal 8:
  Sebuah peta menggunakan skala $1:200.000$. Jika jarak dua kota pada peta adalah $15$ cm, berapakah jarak sebenarnya kedua kota tersebut dalam kilometer?

  Pembahasan:
  Skala $1:200.000$ berarti $1$ cm pada peta mewakili $200.000$ cm pada kenyataan.
  Jarak pada peta $= 15$ cm.
  Jarak sebenarnya $= textJarak pada peta times textnilai skala$
  Jarak sebenarnya $= 15 text cm times 200.000$
  Jarak sebenarnya $= 3.000.000$ cm.

  Sekarang, kita ubah satuan cm ke km. Kita tahu bahwa:
  $100$ cm $= 1$ meter
  $1000$ meter $= 1$ kilometer
  Jadi, $100 times 1000 = 100.000$ cm $= 1$ kilometer.

  Untuk mengubah $3.000.000$ cm ke km, kita bagi dengan $100.000$:
  Jarak sebenarnya $= frac3.000.000 text cm100.000 text cm/km$
  Jarak sebenarnya $= 30$ km.

  Jadi, jarak sebenarnya kedua kota tersebut adalah $30$ kilometer.

5. Aritmetika Sosial (Pendalaman)

Di semester 2, materi aritmetika sosial seringkali diperdalam dengan konsep-konsep seperti untung, rugi, harga pembelian, harga penjualan, persentase untung/rugi, bunga tunggal, dan pajak.

• Konsep Kunci:

  • Harga Pembelian (HP): Uang yang dikeluarkan untuk membeli suatu barang.
  • Harga Penjualan (HJ): Uang yang diterima dari menjual suatu barang.
  • Untung: Terjadi jika HJ > HP. Besarnya untung = HJ – HP.
  • Rugi: Terjadi jika HJ < HP. Besarnya rugi = HP – HJ.
  • Persentase Untung: $(fractextUntungHP) times 100%$
  • Persentase Rugi: $(fractextRugiHP) times 100%$
  • Bunga Tunggal: Bunga yang dihitung berdasarkan modal awal.
  • Pajak: Kontribusi wajib kepada negara yang bersifat memaksa berdasarkan undang-undang.

• Contoh Soal 9:
  Pak Budi membeli sebuah sepeda motor bekas seharga Rp $12.000.000$. Setelah diperbaiki dengan biaya Rp $1.000.000$, motor tersebut dijual seharga Rp $15.000.000$. Berapa persentase keuntungan yang diperoleh Pak Budi?

  Pembahasan:
  Pertama, hitung total modal yang dikeluarkan Pak Budi:
  Total Modal (Harga Pembelian Total) = Harga Beli Motor + Biaya Perbaikan
  Total Modal = Rp $12.000.000$ + Rp $1.000.000$ = Rp $13.000.000$.

  Selanjutnya, hitung keuntungan yang diperoleh:
  Keuntungan = Harga Jual – Total Modal
  Keuntungan = Rp $15.000.000$ – Rp $13.000.000$ = Rp $2.000.000$.

  Terakhir, hitung persentase keuntungan:
  Persentase Keuntungan = $(fractextKeuntungantextTotal Modal) times 100%$
  Persentase Keuntungan = $(fractextRp 2.000.000textRp 13.000.000) times 100%$
  Persentase Keuntungan = $frac213 times 100%$
  Persentase Keuntungan $approx 0.1538 times 100%$
  Persentase Keuntungan $approx 15.38%$

  Jadi, persentase keuntungan yang diperoleh Pak Budi adalah sekitar $15.38%$.

Strategi Belajar Efektif

Untuk menguasai materi matematika kelas 7 semester 2, terapkan strategi berikut:

1. Pahami Konsep Dasar: Jangan terburu-buru mengerjakan soal. Pastikan Anda benar-benar memahami definisi, rumus, dan teorema yang mendasari setiap topik.
2. Latihan Soal Beragam: Kerjakan berbagai macam soal, mulai dari yang mudah hingga yang menantang. Ini akan membantu Anda mengenali pola soal dan cara penyelesaian yang berbeda.
3. Identifikasi Kesalahan: Saat mengerjakan soal, catat di mana Anda melakukan kesalahan. Pahami akar masalahnya agar tidak terulang kembali.
4. Diskusi dengan Teman atau Guru: Jangan ragu untuk bertanya jika ada materi yang belum dipahami. Berdiskusi dengan teman bisa memberikan perspektif baru.
5. Buat Catatan Rangkuman: Buat ringkasan materi dan rumus penting. Ini sangat berguna untuk pengulangan.
6. Gunakan Sumber Belajar Tambahan: Manfaatkan buku paket, buku referensi, video pembelajaran online, atau aplikasi edukasi matematika.

Penutup

Matematika kelas 7 semester 2 menawarkan berbagai konsep menarik yang penting untuk dipelajari. Dengan memahami contoh soal dan pembahasannya secara mendalam, serta menerapkan strategi belajar yang efektif, Anda akan mampu menguasai materi ini dengan baik. Teruslah berlatih, jangan mudah menyerah, dan nikmati proses belajar matematika! Semoga artikel ini bermanfaat dalam perjalanan akademis Anda.